数学が苦手な人でもわかる簡単な『微分』の図解説明

微分とは

まずは『微分』とは『何を求めているのか』を、ざっくりとイメージで掴んでいきましょう。

微分の役割のイメージ

足し算であればいくつ増えたのかを求めています。引き算であればいくつ減ったのかを求めていますよね。では微分は何を求めているのでしょうか。

それは『変化の割合』です。

• 微分が求めるもの ＝『変化の割合』

『変化の割合』とは『グラフの2点を結んだ直線の傾き』のこと。数学っぽい用語で聞くと難しく感じるかもしれませんが簡単な事例を見てみるとすぐに理解できるでしょう。

変化の割合のイメージをつかむ事例

例えば次のような問題を考えてみましょう。10日間でお金が10万円増えました。1日いくらのペースでお金が増えたでしょうか？

答えは1万円ですよね。

10万円を10日間で割れば1日1万円ずつ変化してお金が増えていることがわかります。この1日1万円が『変化の割合』です。これをグラフにすると下記のようになります。

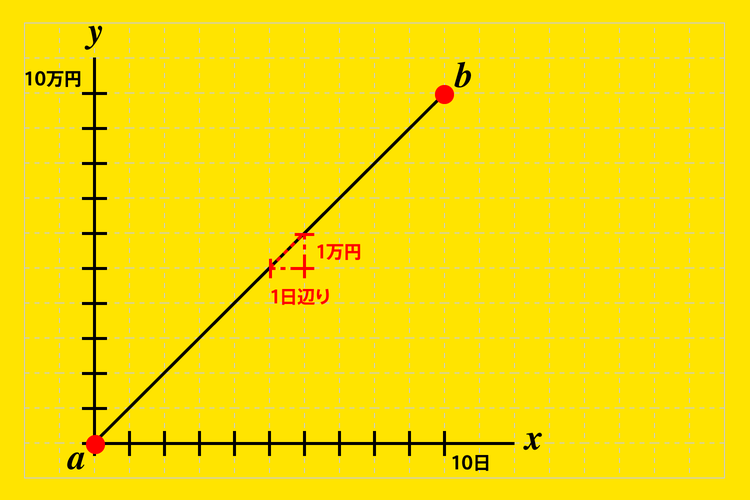
横軸\(x\)が日にちです。0日目から始まり10日目まで。縦軸\(y\)はお金です。0円から始まり10万円まで。\(a\)点（0日目, 0円）〜 \(b\)点（10日目, 10万円）を直線で引いたグラフです。

変化の割合（グラフの2点を結んだ直線の傾き）はこのグラフで言うところの\(a\)点から\(b\)点まで右上にまっすぐに伸びている直線の傾きを求めます。中学1年の数学では『変化の割合』のことを『傾き』と言っていましたね。

『傾き』と『変化の割合』は基本的に同じものです。

『傾き』を求める公式

『傾き』や『変化の割合』を求める公式は以下のようになっています。

• \(\displaystyle 変化の割合 = \frac{yの増加量}{xの増加量}\)

ここで\(x\)の増加量は経過日数（\(10日–0日\)）です。\(y\)の増加量は増えたお金の量（\(10万円–0円\)）ですね。これを先程の式に当てはめます。

• \(\displaystyle 変化の割合 = \frac{10万円–0円}{10日–0日}\)

つまり、

• \(\displaystyle 変化の割合：1万円 = \frac{10万円}{10日}\)

です。

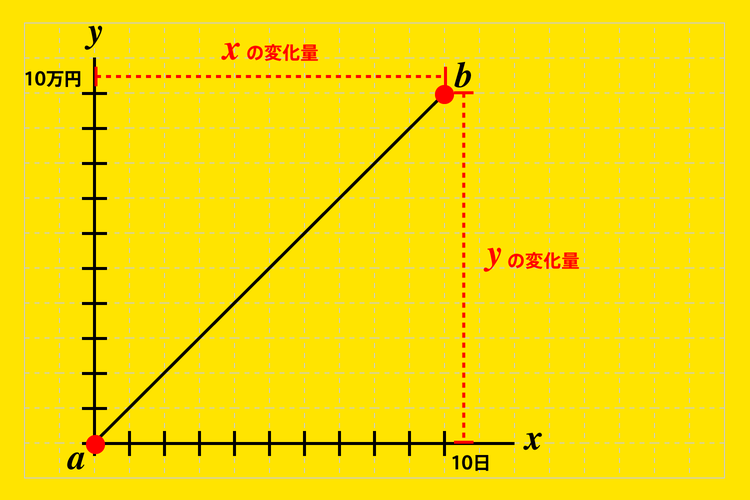
このように『微分』とは『ある期間でどれぐらい変化しているのかという変化量を求めている』とざっくりイメージを掴んでおいてください。

微分が扱う期間はとても細かい

中学の数学で『傾き』から『変化の割合』と呼ばれ方が変わりました。高校数学ではさらに『平均変化率』と言う言葉にかわります。ここからの解説では『平均変化率』を使っていきますが、呼び方が変わっただけですので安心してください。『変化の割合』と同じと考えれば大丈夫です。

『平均変化率』を求めるにはある2点間の変化を計算しますが、『微分』が扱う期間は『微小区間：（ほぼゼロに近いとても細かな期間）』です。次はこのイメージをつかむために曲線グラフから考えてみましょう。

この曲線を描く関数を『\(f(x )\)』とします。

このグラフ上の\(a\)点と\(b\)点の区間が『\(h\)』とすると

• \(a\)：\((x, f(x))\)
• \(b\)：\((x+h, f(x+h))\)

ちょっと記号が増えてきて分かりにくくなってきたのでイメージしやすいように実際に\(x\)に数値を入れてやってみましょう。\(x=2\)とします。

関数\(f(x )\)に\(x=2\)を代入すると\(a、b\)それぞれの座標は以下の通りです。

• \(a\)：\((2, f(2))\)
• \(b\)：\((2+h, f(2+h))\)

平均変化率を求めるには\(a\)点と\(b\)点の2点を結ぶ直線を引きその傾きを計算すればよかったですよね。

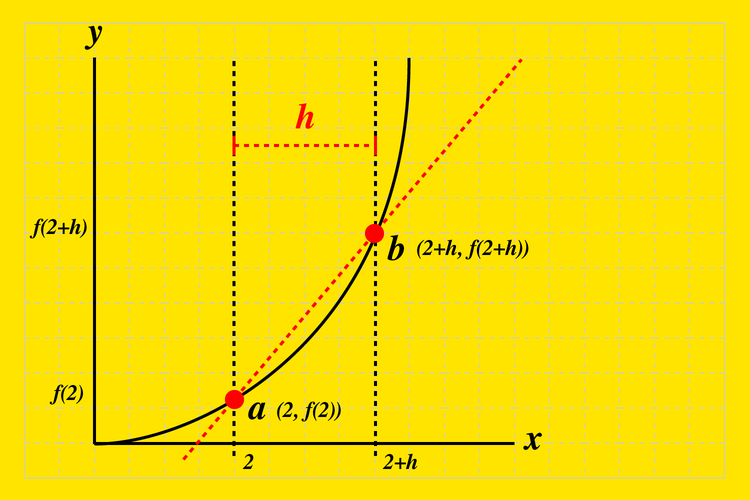
つまり、\(a\)点から\(b\)点の平均変化率（傾き）を求める式は

• \(\displaystyle 平均変化率 = \frac{yの増加量}{xの増加量}\)

ここで\(x\)の増加量は『\((2+h)–2\)』です。\(y\)の増加量は『\(f(2+h)-f(2)\)』です。これを先程の式に当てはめます。

• \(\displaystyle 平均変化率 = \frac{f(2+h)-f(2)}{(2+h)–2}\)

分母の『2』と『-2』は打ち消し合うので『h』のみが残り

• \(\displaystyle 平均変化率 = \frac{f(2+h)-f(2)}{(\cancel{2}+h)–\cancel{2}}\)
  
  ↓
• \(\displaystyle 平均変化率 = \frac{f(2+h)-f(2)}{h}\)

になります。

ここまでは10日で10万円の事例と全く同じですね。

ここからがすごく重要な部分になります。それは『微分が扱う期間はとても細かい』と言うこと。微分は『微小区間（無限に細かい区間）』での『平均変化率』を求めます。

10日で10万円の事例では1日あたりの1万円増えたこと（平均変化率）が求まりましたが、ある瞬間には一体お金がいくら増えていたのかを求めようとしているということです。

\(a\)点と\(b\)点の区間『\(h\)』を微分では限りなくゼロになるように近づけて行きます。

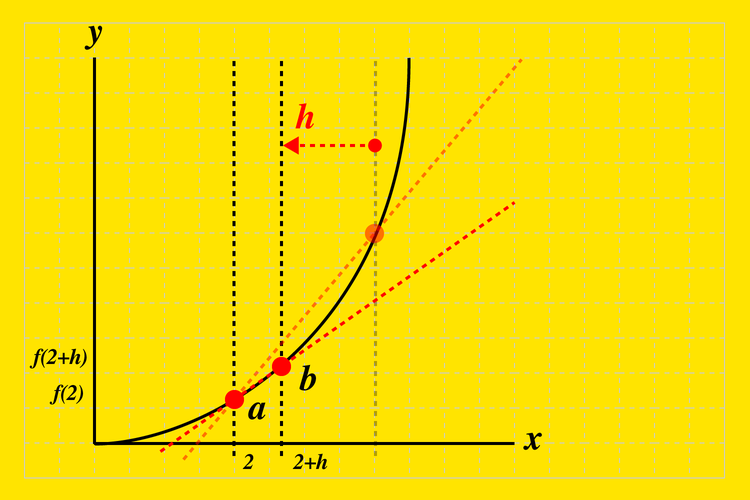
区間『\(h\)』を限りなく近づけていくと2点間を通る直線の傾きは最終的にほぼ曲線の接線となります。

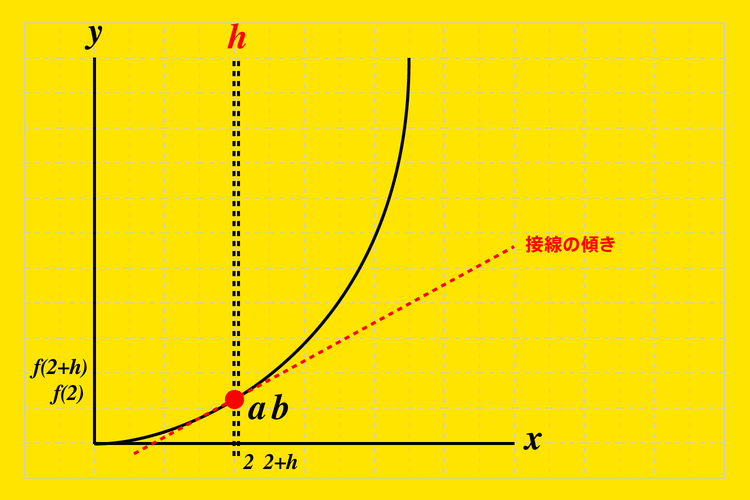
つまり、本来微分によって求められるものはこの『接線の傾き』なのです。

• 『接線の傾き』＝『ある瞬間の平均変化率』

冒頭のざっくりとしたイメージでは

• 微分が求めるもの ＝『変化の割合』

とお伝えしていましたが厳密には

• 微分が求めるもの ＝『接線の傾き（ある瞬間における平均変化率）』

となります。

最初のイメージでは『ある区間の平均変化率』でしたが、厳密には『ある点（無限に細かい区間・微小区間）における平均変化率』とイメージすればよいでしょう。

微分の式と用語

平均変化率の式

• \(\displaystyle 平均変化率 = \frac{f(2+h)-f(2)}{h}\)

を『ある点（無限に細かい区間・微小区間）における平均変化率』の式に変更すると以下のようになります。

• \(\displaystyle f'(2) = \lim_{h \to 0} \frac{f(2+h)-f(2)}{h}\)

\(\displaystyle \lim_{h \to 0}\)の\(\lim\)はlimit（極限）のことで区間『h』を限りなくゼロに近づけることを表しています。

\(f'(2) \)は関数\(f(x)\)の『微分係数』と呼びます。『微分係数』は平均変化率において、区間『h』を限りなくゼロに近づけた時の値です。

そしてここまでイメージしやすいように定数として利用してきた値『\(2\)』を一般的な変数\(x\)に置き換えてみましょう。そうすると次の式になります。

• \(\displaystyle f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\)

定数『\(2\)』を変数\(x\)に置き換えたことで\(f'(x)\)は微分係数を導き出す関数となりました。この\(f'(x)\)のことを『導関数の定義』と呼びます。『導関数』とは微分係数を導き出す関数です。

例えば、\(f(x)=x^2\)の場合

• \(\displaystyle f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\)

上記『導関数の定義』の\(f(x)\)を関数\(f(x)=x^2\)に置き換えます。

• \(\displaystyle f'(x) = \lim_{h \to 0} \frac{(x+h)^2-(x)^2}{h}\)

式を展開すると

• \(\displaystyle f'(x) = \lim_{h \to 0} \frac{x^2+2xh+h^2-x^2}{h}\)

分母の2同士はキャンセルできるので

• \(\displaystyle f'(x) = \lim_{h \to 0} \frac{\cancel{x^2}+2xh+h^2-\cancel{x^2}}{h}\)
  
  ↓
• \(\displaystyle f'(x) = \lim_{h \to 0} \frac{2xh+h^2}{h}\)

さらに分母分子で『h』同士をキャンセルして

• \(\displaystyle f'(x) = \lim_{h \to 0} \frac{2x\cancel{h}+\cancel{h}^2}{\cancel{h}}\)
  
  ↓
• \(\displaystyle f'(x) = \lim_{h \to 0} 2x+h\)

『h』は極限までゼロに近づける事から『h』に0を当てはめ

• \(\displaystyle f'(x) =2x\)

\(\displaystyle f'(x) =2x\)を関数\(f(x)=x^2\)の『導関数（微分係数を導き出す関数）』と呼びます。このように『導関数の定義』などを使ってある関数の導関数を求めることを『微分する』と言います。

『平均変化率』『接線の傾き』『微分係数』『導関数』『微分する』の関係性

用語が一気に増えて少しややこしくなってきたので一旦ここまでの流れと用語を整理しておきましょう。

ある2点\(a、b\)を通る直線の傾きを『平均変化率』。平均変化率を求める式は

• \(\displaystyle 平均変化率 = \frac{yの増加量}{xの増加量}\)

なので

• \(\displaystyle 平均変化率 = \frac{f(2+h)-f(2)}{h}\)

になります。分母は2同士がキャンセルされています。（\((\cancel{2}+h)–\cancel{2}\)）

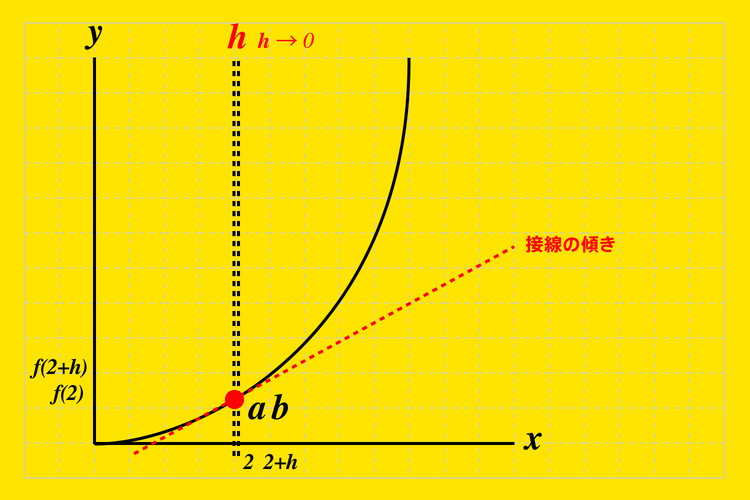
\(a、b\)の2点間『\(h\)』を限りなくゼロに近づける（\(\displaystyle \lim_{h \to 0}\)）と\(a、b\)を通る直線の傾きは『接線の傾き』となり、式が

• \(\displaystyle f'(2) = \lim_{h \to 0} \frac{f(2+h)-f(2)}{h}\)

で、関数\(f(x)\)の\(x=2\)における微分係数は\( f′(2)\)となります。

そして定数『\(2\)』を一般的な変数\(x\)に置き換えると微分係数を導き出す『導関数の定義』になります。

• \(\displaystyle f'(x) = \lim_{h \to 0} \frac{(x+h)^2-x^2}{h}\)

実際に\(f(x)=x^2\)を『導関数の定義』を使って『微分する』と関数\(f(x)\)の『導関数』は

• \(\displaystyle f'(x) = \lim_{h \to 0} 2x\)

となり、例えば\(x=3\)のとき

• \(\displaystyle f'(x) = \lim_{h \to 0} 2*3\)

関数\(f(x)\)の\(x=3\)における微分係数は

• \(\displaystyle f'(3) = 6\)

つまり、関数\(f(x)\)の\(x=3\)における『接線の傾き』は『\(6\)』と求まりました。

今日のdot

『微分』とはある瞬間における平均変化率『接線の傾き』が求まります。

• 微分で求まるもの ＝『接線の傾き』

ある関数を『微分する』と『導関数』が求まり、導関数に定数を代入すると『微分係数』が求まります。

『微分する』には『導関数の定義』か『微分の公式』を利用することで求めることができます。

導関数の定義

• \(\displaystyle f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\)