
Numpyで正規分布の乱数配列を生成するrandn、normalを徹底解説
- 公開日:2019/08/08
- 更新日:2019/08/08
- 投稿者:n bit
Numpyのrondomモジュールで標準正規分布の乱数配列を生成するrandnメソッドと、μ(平均)とσ(標準偏差)を任意で指定した正規分布の乱数配列を生成するnomalメソッドについて、出力値をグラフにプロットしながら徹底解説します。
この記事は約 分で読めます。(文字)
正規分布の概要
Numpyのランダムモジュールの中でも正規分布に従う乱数の配列を生成するメソッドrandnとnormalについて解説します。まずは正規分布の概要について少しおさらいしておきましょう。
正規分布はガウス分布とも呼ばれ以下の確率密度関数に従います。
\(\displaystyle f(x; \mu,\sigma^2)=\frac{1}{ \sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma ^2}\right) \: (x \in R)\)
\(\mu\)は平均値で、\(\sigma^2\)は分散、\(\sigma\)は標準偏差でしたね。
正規分布の分布はこの\(\mu\)(平均値)と、\(\sigma^2\)(分散)によって決まります。
標準正規分布の乱数配列を生成する
randn
正規分布の中でも\(\mu\)(平均値)=0、\(\sigma^2\)(分散)=1の分布を標準正規分布と呼びます。Numpyで標準正規分布の乱数配列を生成するのはrondomモジュール内の【randn】メソッドです。
利用するには最初にNumpyをインポートしておきましょう。
import numpy as np
1次元配列を標準正規分布の乱数で生成
randnは\(\mu\)と、\(\sigma^2\)が固定ですので基本的には乱数の生成サイズのみ指定してやれば利用できます。
引数に何も設定しない場合は標準正規分布に従う値を1つ生成します。
s1 = np.random.randn()
print(s1)
出力結果
-0.4690374291384017
出力する乱数の生成サイズを指定したい場合は引数に数値を指定します。引数に10を指定すると出力されるのは標準正規分布に従った10の要素を持つ乱数配列です。
s10 = np.random.randn(10)
print(s10)
出力結果
[ 0.25702137 0.397795 0.54809017 -0.07603311 0.15085285 -0.11272486
0.25232319 0.48244184 0.89100164 -2.54745675]
行列を標準正規分布の乱数で生成
引数に値を2つ設定することで行列を出力することも可能です。下記事例では2×3行列を出力しました。
s2_3 = np.random.randn(2,3)
print(s2_3)
出力結果
[[-0.44054578 -2.46724828 0.40256177]
[-0.20914594 0.8348336 -0.10013049]]
多次元行列を標準正規分布の乱数で生成
また、引数に複数の値を設定することで多次元行列を出力することもできます。
s2_2_3 = np.random.randn(2,2,3)
print(s2_2_3)
出力結果
[[[ 0.27525156 -1.17074296 -0.76404884]
[-0.47703543 -1.87440015 -0.3852637 ]]
[[ 0.81742412 -1.16274058 1.42167577]
[ 0.86729486 -1.79801214 0.4235013 ]]]
1次元の標準正規分布とrandnで出力した配列の比較
出力された分布を実際にヒストグラムに出力して確認してみましょう。
# 標準正規分布 (平均0, 分散1)
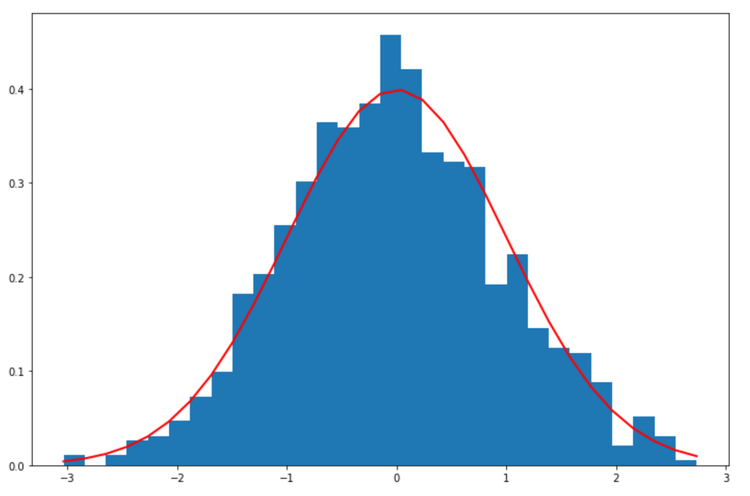
s1 = np.random.randn(1000)
青のヒストグラムがrandnから出力された配列を出力したものです。赤の実線は標準正規分布。同じように分布していることが確認できますね。
平均と標準偏差を指定した正規分布の乱数配列を生成する
normal
【normal】メソッドは、randnと違い、\(\mu\)(平均値)と\(\sigma\)(標準偏差)を任意で指定した正規分布に従う乱数配列を生成することができます。\(\sigma^2\)(分散)ではなく\(\sigma\)(標準偏差)で指定していることに注意してください。
利用する引数は以下の3つです。
- loc:\(\mu\)(平均値)
- col:\(\sigma\)(標準偏差)
- size:乱数配列の生成サイズ
sizeの指定に関してはrandnと基本的に同じ考え方になります。
1次元配列を正規分布の乱数で生成
normalは\(\mu\)と、\(\sigma\)を指定して、乱数の生成サイズを指定してやれば利用できます。下記は\(\mu\)(平均値)=0、\(\sigma\)(標準偏差)=3の出力事例です。
sizeを設定しない場合は正規分布に従う値を1つ生成します。
s1 = np.random.normal(loc=0, scale=3)
print(s1)
出力結果
-1.5803453871138342
出力する乱数の生成サイズを指定する場合はsizeに数値を指定します。sizeに10を指定すると出力されるのは正規分布に従った10の要素を持つ乱数配列です。
s10 = np.random.normal(loc=0, scale=3, size=(10))
print(s10)
出力結果
[ 1.32157688 1.19379194 -3.4622456 -2.28158956 1.51044475 5.00503209
-1.34903914 -4.02156345 0.19300375 1.09009916]
行列を正規分布の乱数で生成
乱数で行列を生成する場合はsizeに行と列の値を指定します。下記事例では2×3行列を出力しました。
s2_3 = np.random.normal(loc=0, scale=3, size=(2,3))
print(s2_3)
出力結果
[[-1.75038197 -0.57937312 -7.70167643]
[-2.02146828 -8.39138393 2.86930953]]
多次元行列を正規分布の乱数で生成
また、sizeに複数の値を設定することで多次元行列を出力することもできます。
s2_2_3 = np.random.normal(loc=0, scale=3, size=(2,2,3))
print(s2_2_3)
出力結果
[[[-0.70081984 -0.42181109 1.28025032]
[ 6.69168281 1.56132419 0.9131835 ]]
[[ 1.06685883 -1.58767083 -0.05535416]
[-2.477204 -0.99822221 4.86036055]]]
1次元の正規分布とnormalで出力した配列の比較
出力された分布を実際にヒストグラムに出力して確認してみましょう。今回は\(\mu\)(平均)と、\(\sigma^2\)(分散)を以下の3種類それぞれに設定して出力しています。
- \(\mu\)(平均値)=0、\(\sigma^2\)(分散)=2
- \(\mu\)(平均値)=0、\(\sigma^2\)(分散)=1
- \(\mu\)(平均値)=0、\(\sigma^2\)(分散)=0.5
出力するときはそれぞれ\(\sigma^2\)(分散)の\(\sqrt{}\)をとって\(\sigma\)(標準偏差)に戻しています。
# 標準正規分布 (平均0, 分散2)
s1 = np.random.normal(loc=0, scale=np.sqrt(2), size=1000)
# 標準正規分布 (平均0, 分散1)
s2 = np.random.normal(loc=0, scale=np.sqrt(1), size=1000)
# 標準正規分布 (平均0, 分散0.5)
s3 = np.random.normal(loc=0, scale=np.sqrt(0.5), size=1000)
青のヒストグラムと、赤の実線がnormalから出力された配列を出力したものです。赤の点線は正規分布。それぞれ\(\mu\)(平均)と、\(\sigma^2\)(分散)の指定により分布の違いが確認できます。
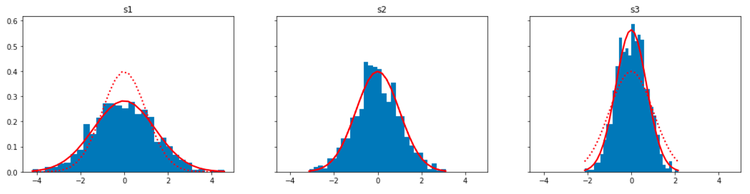
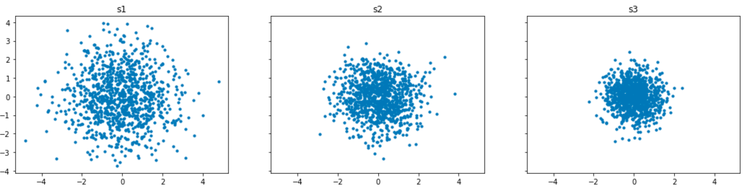
下記はx,y軸それぞれ同じ\(\mu\)(平均)と、\(\sigma^2\)(分散)を指定した2次元の散布図です。上記の1次元ヒストグラムと同じで分散具合に違いがあることが確認できます。
今日のdot
正規分布は自然界で頻繁に発生する確率分布で分析・統計、機械学習などの場面で頻繁に利用するのでこれを機会にしっかりとマスターしておきましょう。
【フリーランス向けの完全無料Pythonプログラミング講座】
dot blogではこの記事以外にも完全無料でフリーランス向けのPythonプログラミング講座を公開中です。フリーランスとして活躍し稼ぐための強力な武器となりますよ。

Python入門講座【無料のプログラミング学習講座】
最近特に注目度が高くなってきているプログラミング言語Python。転職、フリーランス、独立・起業を検討中、日々の業務が忙しい社会人等は今こそ身に付けておきたいスキルの1つ。初心者向けにやさしいプログラミング学習内容のPython入門講座を無料で公開。


