加重移動平均（WMA）と指数移動平均（EMA）とは。SMAとの違い

加重移動平均と指数移動平均の概要

こちらのページでは単純移動平均線について解説しました。

単純移動平均線【SMA：Simple Moving Average】とは

チャートのテクニカル分析においてはかなりの頻度で利用されている単純移動平均線【SMA：Simple Moving Average】。単純移動平均線の特徴やその求め方、また、トレードにおいての活用法、現状のトレンドの見極め方などを解説しています。

この記事を読む ≫

単純移動平均線はテクニカル分析の指標として数多くのトレーダーに利用されていますが、この指標にはメリットばかりではなくデメリットも存在しています。

単純移動平均線のデメリットをカバーするための指標として加重移動平均線や指数移動平均線などが考案されました。加重移動平均線と指数移動平均線も単純移動平均線と同じく主にトレンドフォローを分析する指標として利用されています。

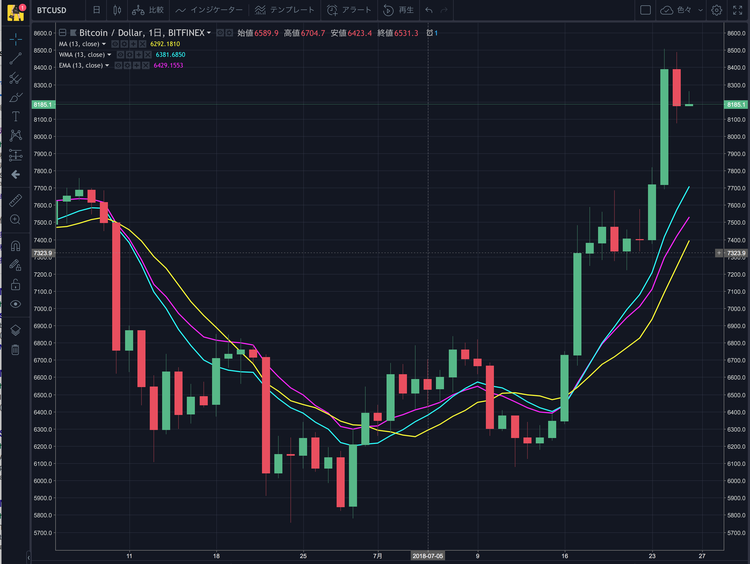
下記のチャート上には単純移動平均線、加重移動平均線、指数移動平均線の3本をローソク足上に配置しています。期間は全て13設定です。

• 単純移動平均線【SMA：Simple Moving Average】：黄色
• 加重移動平均線【WMA：Weighted Moving Average】：水色
• 指数移動平均線【EMA：Exponentially Moving Average】：ピンク色

単純移動平均線【SMA：Simple Moving Average】のデメリット

単純移動平均線には大きく分けて2つのデメリットが存在します。

• 1つ目のデメリットは単純移動平均線の求める期間内の値動きしか指標のソースとして考慮されていないこと。
• 2つ目のデメリットは各期間内の値に対する重み付けが全て同じであるということ。

1つ目のデメリットに関しては、たとえば日足のSMA10で指標を見るとしても今後の値動きというのは直近10日間の値動きだけによって影響してくるわけでは当然ありません。それ以前の値動きも現在の値動きに影響しています。

そのため、直近10日間だけの情報を元に売買の方向性を決める指標として扱ってよいのかという疑問が出てきますよね。

2つ目のデメリットに関しては、SMA10で直近10日間の全ての終値が同じ価値で直近の値段を判断する指標のソースとして扱われています。しかし自分がトレードする時を思い出してもらえれば分かると思いますが直近10日間の中でもより当日に近い足の動きの方を重要視していることが多いですよね。特に前日の値動きなどは注目している方が多いのではないでしょうか。

加重移動平均線【WMA：Weighted Moving Average】

この2つ目のデメリット全期間の全ての終値を同じ重み付けで扱うというデメリットの解決になるとして考えられたのが『加重移動平均線【WMA：Weighted Moving Average】』です。

加重移動平均【WMA：Weighted Moving Average】の求め方

加重移動平均線は加重移動平均値を求め線で繋いだものです。加重移動平均値の求め方は日足チャート『WMA10, close』を算出事例として説明していきます。

期間が10、値が終値ですので、通常の移動平均であれば本日を含めて直近10日間の終値を全て足し合わせ10（10日間）で割ることで本日の移動平均値を求めることができます。単純移動平均で解説した内容です。

単純移動平均線【SMA：Simple Moving Average】とは

チャートのテクニカル分析においてはかなりの頻度で利用されている単純移動平均線【SMA：Simple Moving Average】。単純移動平均線の特徴やその求め方、また、トレードにおいての活用法、現状のトレンドの見極め方などを解説しています。

この記事を読む ≫

移動平均値の計算式

• \(\displaystyle \frac{ 本日の終値 + 昨日の終値 + ・・・ + 8日前の終値 + 9日前の終値 }{ 10 }\)

加重移動平均では、1番直近の終値を10倍、その前日の終値を9倍、そのまた前日の終値を8倍と10から1ずつ減らしながら掛け算を行い、最終9日前の終値を1倍してすべての合計を足し合わせ55で割ることで本日の加重移動平均値を求めることができます。

加重移動平均値の計算式

• \(\displaystyle \frac{ (本日の終値 × 10) + (昨日の終値 × 9) + ・・・ + (9日前の終値 × 1) }{ 55 }\)

55という数字は1番直近の終値に掛けた10から9日前の値に掛けた1までを全て足し合わせた数字です。足し合わせる終値の数を倍数にしていくことになるので、合計値を割る日数も倍数分の日数にしてあげる必要があります。

• \(55=10+9+8+・・・+1\)

もしピンときにくい場合は2日間の加重移動平均で考えるとわかりやすいと思います。本日の終値に2を掛けて前日の値に1を掛けることになります。つまり、本日の終値を2回足した合計3日間の平均値を求めることになります。

\(2＋1=3\)

2と1をかけた本日と前日の終値の合計を3日で割ることでWMA2を求めたことになるのです。

加重移動平均線のことを『WMA：Weighted Moving Average』と言いますが例えばWMA13であれば13日間の加重移動平均値を求めていることになります。

指数移動平均線【EMA：Exponentially Moving Average】

加重移動平均線は結局のところ単純移動平均線のデメリットを一つしか解決できていません。単純移動平均線の1つ目のデメリット「期間内のデータしか市場の判断に使っていない問題」が残っています。

そこで、直近の終値に重みを付けながらも期間外のデータも考慮に入れようとしたのが指数移動平均線になります。

指数移動平均線【EMA：Exponentially Moving Average】の求め方

指数移動平均値を求める計算式はややこしくなるので簡単に概要だけつかめるようにすると以下のような式になります。

指数移動平均値の計算式

• \(\alpha (今日の終値-前日のEMA)+前日のEMA\)

\(\alpha\)は重みの減少度合いを決める『平滑化係数』と呼ばれるものです。平滑係数は下記の色で求めることができます。

平滑化係数の計算式

• \(\displaystyle \frac{2}{n+1}\)

\(n\)は期間になりますので例えばEMA19であれば

• \(\displaystyle \frac{2}{19+1}\)

で\(0.1\)です。

ある地点のEMAを求めるのに前日のEMAの値を利用しますので連続した計算が行われ理論的にはすべての足の終値が現在の終値に対するEMAに影響してくることになりますが、現実的にそのような計算は難しいので実際には限りなく近い値が求められるように作られています。

指数移動平均線【EMA：Exponentially Moving Average】の重みの付け方

指数移動平均線は加重移動平均線と同じように直近の値に強めの重みを与えます。そのため指数移動平均線は加重移動平均線の一種と言えます。

重みの加えかたは加重移動平均線が過去の終値に向かうにつれ一定量ずつ重みを減少させて加えていったのに対し、指数移動平均値は過去の終値へ向かうにつれ指数関数的に重みを減少させていくことで加重しています。

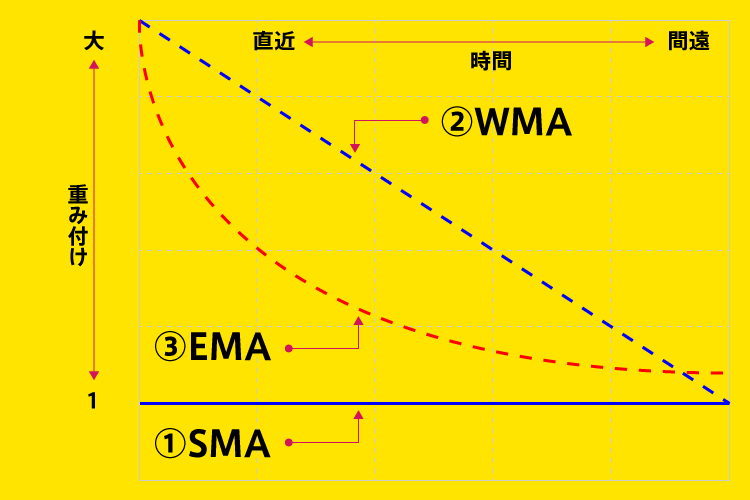
指数と言う言葉が頻繁に出てきますが、上記の図の③EMAの様に指数関数的に重みを加えると言う事は曲線的に加える重みを減少させています。（直近から間遠）

①SMAは重み付けが常に1ですので1のところで横に一直線となります。

②WMAは重み付けが一定量ずつ減少していきますので右肩下がりの1直線となります。

そのため、EMAはSMAやWMAに比べより直近の終値を重要視した指標といえます。

SMA、WMA、EMAの特徴と違い、使い方

ここまでの内容踏まえ再度チャートに反映したSMA、WMA、EMAを見ながら特徴や違い、使い方をつかんでいきましょう。

• 単純移動平均線【SMA：Simple Moving Average】：黄色
• 加重移動平均線【WMA：Weighted Moving Average】：水色
• 指数移動平均線【EMA：Exponentially Moving Average】：ピンク色

まず基本的な使い方は単純移動平均線の使い方と大きな違いはありません。

単純移動平均線【SMA：Simple Moving Average】を使ったトレードタイミング

• 買い：移動平均線をろうそく足が下から上へと抜けていく
• 売り：移動平均線をろうそく足が上から下へと抜けていく

単純移動平均線【SMA：Simple Moving Average】を使ったトレンド判定

• 上昇トレンド：（長期間）移動平均線の上側にローソク足がある
• 下降トレンド：（長期間）移動平均線の下側にローソク足がある

その上でそれぞれの特徴や違いによって向き不向きが見えてきます。

直近の値動きに対するレスポンスの違い

EMAやWMAはSMAに比べより直近の終値に近い値ほど重要視していますのでチャートの動きに対してより反応よく動いていることがわかります。特により直近の終値に大きめの重み付けをしているEMAはWMAに比べてもより反応よく動きます。

• SMA < WMA < EMA

直近のトレンドに対する傾向の違い

EMAやWMAはSMAに比べ算出期間内の終値に対し重み付けを行うためトレンドに対する傾向が強く出やすくなります。特に期間内の終値に対し一定量で強く重み付けを行うWMAはEMAに比べてさらに強い傾向が出ます。

• SMA < EMA < WMA

指数移動平均線【EMA：Exponentially Moving Average】のメリット・デメリット

指数移動平均線は値動きに対するレスポンスが良く当日の指数移動平均値は必ず前日の移動平均値と当日の終値の間に来ると言う特徴があり、指数移動平均線の向きが上向きの間は終値が常に指数移動平均線の上にくる、指数移動平均線の向きが下向きの間は終値が常に指数移動平均線の下にくるようになります。

• 指数移動平均線の向きが上向きの間は終値が常に指数移動平均線の上
• 指数移動平均線の向きが下向きの間は終値が常に指数移動平均線の下

そのためトレンドの転換点の見極めには非常に有効的に働きます。

ただしレスポンスがよすぎる面もありトレンドが弱い時やレンジ相場の時は特にダマシサインが多くなる傾向があります。下記画像中央部分あたりで値動きの方向性が弱い時に終値（赤線上の赤丸）が指数移動平均線（ピンク線）の上下を行き来しているのが分かります。

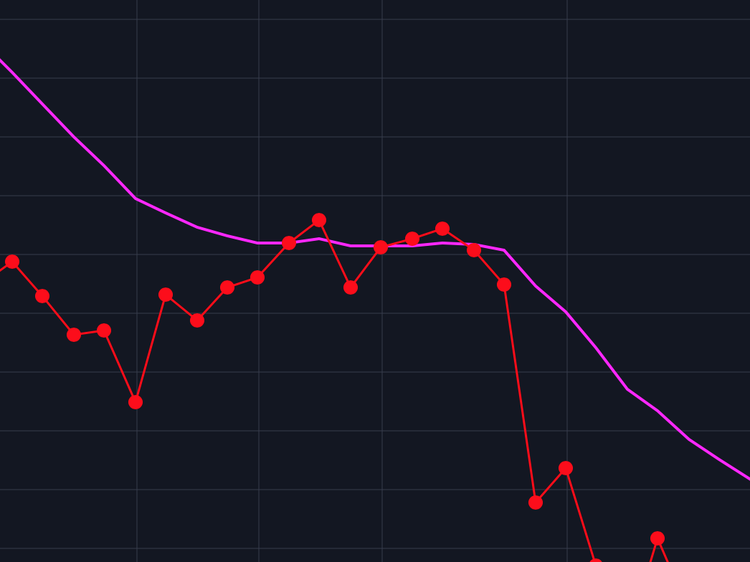
赤：値動きの終値のみを示したもの　ピンク：EMA

• メリット：トレンドの転換点の見極め等に強い
• デメリット：レスポンスが良い分ダマシが多くなりやすい

加重移動平均線【WMA：Weighted Moving Average】のメリット・デメリット

指数移動平均線はどちらかと言うとトレンドフォローの中でも値動きに重視した指標でしたが、加重移動平均線はトレンドフォローの角度や方向性に重視した指標といえます。

下記画像は先ほどと同じ値動きのチャートになりますが中央付近の値動きが弱いところでも加重移動平均線（水色線）は上昇トレンド傾向にあることがわかります。

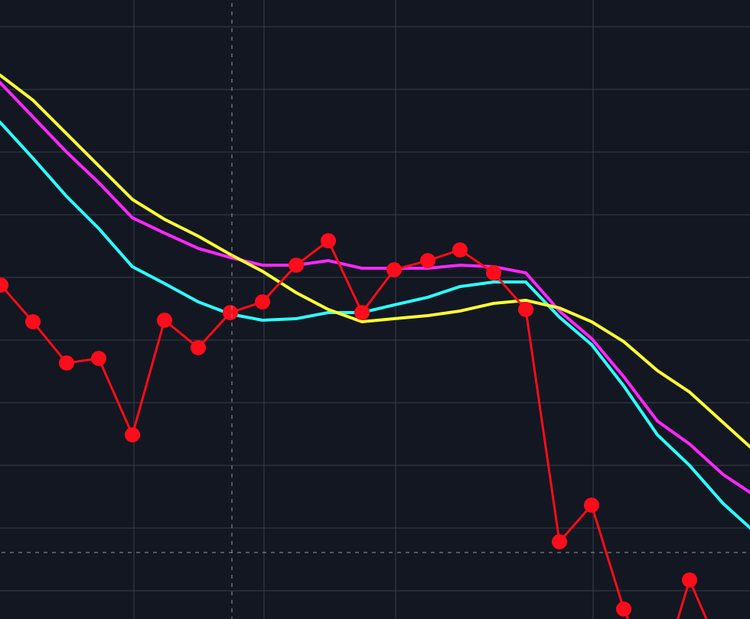
赤：値動きの終値のみを示したもの　ピンク：EMA　水色：WMA　黄色：SMA

加重移動平均線も指数移動平均線と同じで値動きやトレンドに対するレスポンスが良いため売買サインとしてはやはりダマシが出やすくなります。

• メリット：緩やかな値動きでもトレンドの方向性を早く掴むことができる
• デメリット：レスポンスが良い分ダマシが多くなりやすい

単純移動平均線【SMA：Simple Moving Average】のメリット・デメリット

指数移動平均線と加重移動平均線は単純移動平均線のデメリットをカバーするために考案されたものですので、単純移動平均線のメリットデメリットはそれらの逆になります。

• メリット：ダマシサインが出にくく大きなトレンドをつかみやすい
• デメリット：レスポンスが遅いので売買サインとしては遅れがち

今日のdot

単純移動平均線のデメリットをカバーするために考案された指数移動平均線や加重移動平均線ですが、それらも決して完璧ではなくデメリットは残っています。結局は市場の値動きなどに合わせてどれを利用するか、そして、トレンドの転換点やトレンドフォローの強さなど自分が得たい情報、それに合わせて利用する売買戦略等によって利用する指標を検討していく必要があります。

また、多くのトレーダーの方が利用している指標に関しては意識されやすいラインとなり売買サインとしても扱いやすいものとなります。どんなテクニカル分析指標が多く利用されているのか、そしてどのような区間で利用されているのかなども重要ですね。