Pythonで単純移動平均線【SMA：Simple Moving Average】を算出するのイメージ画像

Pythonで単純移動平均線【SMA：Simple Moving Average】を算出する

  • 公開日：2018/07/06
  • 更新日：2018/10/19
  • 投稿者：n bit

Pythonで単純移動平均値の算出や単純移動平均線の描画を行います。単純移動平均線を使ったトレードルールは容易に設定することができ、かつ、具体的な売買シグナルを出すことができるためbotなどの自動取引を行うプログラミングと非常に相性の良いテクニカル分析指標です。

  • Python
  • bot
  • テクニカル分析

この記事は約 分で読めます。（文字）

Pythonで単純移動平均線【SMA：Simple Moving Average】を算出

単純移動平均線【SMA：Simple Moving Average】はトレンドフォロー系のテクニカル分析指標です。現状のトレンドの見極めや、トレンド転換に対する売買シグナルなどを求めることができます。

単純移動平均線の詳しい概要や活用方法などを知りたい方は下記のページで解説していますのでご覧になってください。

単純移動平均線【SMA：Simple Moving Average】とは

チャートのテクニカル分析においてはかなりの頻度で利用されている単純移動平均線【SMA：Simple Moving Average】。単純移動平均線の特徴やその求め方、また、トレードにおいての活用法、現状のトレンドの見極め方などを解説しています。

この記事を読む ≫

単純移動平均線【SMA：Simple Moving Average】の計算式

移動平均とは、時系列データで算出時点からある期間の過去の直近データの平均値を求めたものになります。例えば1時間足で10期間の移動平均を求める場合、各ローソク足ごとに直近10時間分のデータを足し合わせて10 (10時間)で割ることで起点となったローソク足の移動平均値を求めることができます。

移動平均値の計算方法

  • \(\displaystyle \frac{ 現時点の終値 + 1時間前の終値 + ・・・ + 9時間前の終値 }{ 10 }\)

ローソク足が1本ごと移るたび、移動平均の計算に利用される10本のローソク足も1つずつ移動していきます。算出期間が移動していく平均値の計算法と言う意味で『移動平均』と呼ばれていて、このような計算方法を『ローリング計算』とも呼びます。

  • \(\displaystyle SMA_(t) = \frac{Close_(t)+Close_(t-1)+ ・・・ +Close_(t-n+1)}{n}\)
  • \(SMA_(t)\)：現時点の移動平均値
  • \(Close\)：終値
  • \(t\)：現時点
  • \(n\)：算出期間

この各ローソク足の移動平均値を線でつないでいくことで単純移動平均線を引くことができます。

Pyhonで単純移動平均線【SMA：Simple Moving Average】を計算する

Pythonで移動平均値を求めるときにいちいち計算式を書かなくてもローリング計算を行うための専用メソッドがpandasの中に用意されています。今回はpandasの『rolling』メソッドを利用します。

使い方は非常に簡単です。データフレーム形式のohlcvデータを、算出期間を引数に持った『rolling』メソッドで計算させます。ローリング計算の計算方法を平均にするため後に『mean()』をつけます。

sma = df_ohlcv['close'].rolling(10).mean()

『rolling』メソッドの引数に設定している『10』は算出期間です。『sma』には計算された『移動平均値』が返されます。

さすがpandas。とてもコードがシンプルですね。

Pyhonとmatplotlibで単純移動平均線【SMA：Simple Moving Average】を描画するソースコード

matplotlibを使って単純移動平均線【SMA：Simple Moving Average】を描画してみましょう。下記は単純移動平均線を描画する最低限のソースコードとなっています。

ソースコード

データフレーム『df_ohlcv』は、

  • date：datetime形式の日時データ
  • open：始値
  • hight：高値
  • low：安値
  • close：終値
  • volume：出来高

の値を持っています。

基本構造

#-*- coding:utf-8 -*-

import pandas as pd

import mpl_finance as mpf

from collections import OrderedDict

import matplotlib

import matplotlib.pyplot as plt



# 日時データをDataFrameのインデックスにする

df_ohlcv = df_ohlcv.set_index('date')



# 移動平均（SMA：Simple Moving Average）の算出（期間10）

df_sma = pd.DataFrame(OrderedDict({

                            'SMA10':  df_ohlcv['close'].rolling(10).mean(),

                        }))



# 描画領域を作成

fig = plt.figure(figsize=(20,20))

ax = plt.subplot(1,1,1)



# チャート表示数にDataFrameをトリミング

df_ohlcv = df_ohlcv.iloc[-121:]

df_sma   = df_sma.iloc[-121:]



# ロウソクチャートをプロット

mpf.candlestick2_ohlc(ax,

                      opens     = df_ohlcv["open"],

                      highs     = df_ohlcv["high"],

                      lows      = df_ohlcv["low"],

                      closes    = df_ohlcv["close"],

                      width     = 0.8,

                      colorup   = "#46AE74",

                      colordown = "#E4354A")



# x軸をdateにする

xdate = df_ohlcv.index 

x_int_list = range(0, len(xdate), 6)

ax.set_xticks(x_int_list)

ax.set_xticklabels((xdate[int(x)].strftime('%d %H:%M') for x in x_int_list))



# グラフの両サイドをトリム

ax.set_xlim([-1, 121])



# 移動平均（SMA：Simple Moving Average）をプロット

df_sma.reset_index(inplace=True)

ax.plot(df_sma['SMA10'], color='Blue', linewidth='1.0', label='SMA10')



# x軸の整形 

fig.autofmt_xdate(bottom=0.2, rotation=30, ha='right')



# グラフの描画

plt.show()

class版

こちらは上記の行動class化したものです。複雑に見えるかもしれませんがやっている事は上記の基本構造と同じ事しかやっていません。ohlcvの取得、SMAの計算、グラフへのプロットと言う3つの工程をそれぞれ関数に分けています。

現状はあまり汎用性の高い組み方ではありませんが、個別に関数化しているため使い回しはしやすいと思います。

from datetime import datetime as dt

import requests, pytz

import pandas as pd

import mpl_finance as mpf

from collections import OrderedDict

import matplotlib

import matplotlib.pyplot as plt





class TechnicalAnalysis:



    def __init__(self):

        # 初期設定

        self.REQUESTS_URL = 'https://www.bitmex.com/api/udf/history?symbol=XBTUSD&resolution={t_res}&from={t_from}&to={t_to}'





    def df_ohlcv(self, time_range=60, bar_no=500):

        # ohlcvの取得

        t_to = int(dt.now(pytz.utc).timestamp())

        t_from = t_to - time_range * 60 * bar_no

        row_ohlcv = requests.get(self.REQUESTS_URL.format(t_res=time_range, t_from=t_from, t_to=t_to))

        json_ohlcv = row_ohlcv.json()

        list_ohlcv = [list(ohlcv) for ohlcv in zip(json_ohlcv["t"], json_ohlcv["o"], json_ohlcv["h"], json_ohlcv["l"], json_ohlcv["c"], json_ohlcv["v"])]

        df_ohlcv = pd.DataFrame(list_ohlcv, columns=["timestamp", "open", "high", "low", "close", "volume"])



        # 日時データをDataFrameのインデックスにする

        df_ohlcv["datetime"] = pd.to_datetime(df_ohlcv["timestamp"], unit="s")

        df_ohlcv = df_ohlcv.set_index("datetime")

        pd.to_datetime(df_ohlcv.index, utc=True)



        return df_ohlcv





    def ta_sma(self, df_ohlcv, ma_range=10):

        # 移動平均（SMA：Simple Moving Average）の算出

        df_key = 'SMA' + str(ma_range)

        df_sma = pd.DataFrame(OrderedDict({

                                    df_key: df_ohlcv['close'].rolling(ma_range).mean(),

                                }))



        return df_sma





    def ta_sma_plot(self, df_ohlcv, df_sma, ma_range=10, bar_no=120):

        # 描画領域を作成

        fig = plt.figure(figsize=(20,20))

        ax = plt.subplot(1,1,1)



        # チャート表示数にDataFrameをトリミング

        df_ohlcv = df_ohlcv.iloc[-(bar_no)-1:]

        df_sma   = df_sma.iloc[-(bar_no)-1:]



        # ロウソクチャートをプロット

        mpf.candlestick2_ohlc(ax,

                              opens     = df_ohlcv["open"],

                              highs     = df_ohlcv["high"],

                              lows      = df_ohlcv["low"],

                              closes    = df_ohlcv["close"],

                              width     = 0.8,

                              colorup   = "#46AE74",

                              colordown = "#E4354A")



        # x軸をdateにする

        xdate = df_ohlcv.index 

        x_int_list = range(0, len(xdate), 6)

        ax.set_xticks(x_int_list)

        ax.set_xticklabels((xdate[int(x)].strftime('%d %H:%M') for x in x_int_list))



        # x軸の整形 

        fig.autofmt_xdate(bottom=0.2, rotation=30, ha='right')



        # グラフの両サイドをトリム

        ax.set_xlim([-1, bar_no+1])



        # 移動平均（SMA：Simple Moving Average）をプロット

        df_sma.reset_index(inplace=True)

        df_key = 'SMA' + str(ma_range)

        ax.plot(df_sma[df_key], color='Blue', linewidth='1.0', label=df_key)



        # グラフの描画

        plt.show()





def main():

    ma_range=10

    ta = TechnicalAnalysis()

    df_ohlcv = ta.df_ohlcv(time_range=60, bar_no=500)

    df_sma = ta.ta_sma(df_ohlcv, ma_range=ma_range)

    ta.ta_sma_plot(df_ohlcv, df_sma, ma_range=ma_range, bar_no=120)





if __name__ == '__main__':

    main()

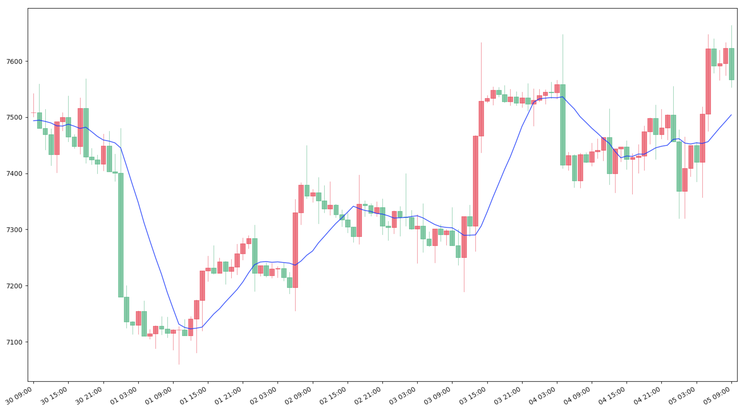
出力結果

ロウソクチャートの上側にブルーの単純移動平均線が描画されていることが確認できます。

Pythonで単純移動平均線【SMA：Simple Moving Average】を算出1

今日のdot

単純移動平均線【SMA：Simple Moving Average】を求めるには『ローリング計算』を利用します。

  • \(\displaystyle SMA_(t) = \frac{Close_(t)+Close_(t-1)+ ・・・ +Close_(t-n+1)}{n}\)
  • \(SMA_(t)\)：現時点の移動平均値
  • \(Close\)：終値
  • \(t\)：現時点
  • \(n\)：算出期間

Pythonではpandasの『rolling().mean()』メソッドで『ローリング計算』を行うのが簡単です。

sma = df_ohlcv['close'].rolling(10).mean()

『rolling().mean()』メソッドによる『ローリング計算』で算出した各ローソク足の移動平均値を線でつないでいくことで単純移動平均線を描画します。

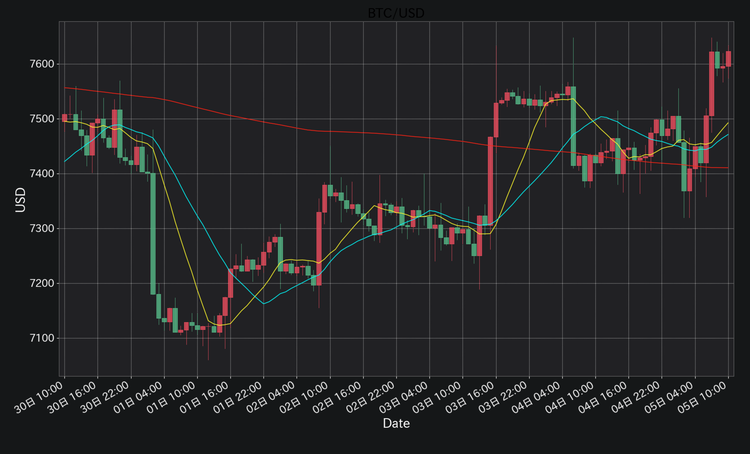
サンプルコードでは極力わかりやすいように最低限のコードのみにしています。複数の単純移動平均線をプロットする事で短期、中期、長期といった単純移動平均線の1つのグラフ内に表示させることもできます。後は、matplotlibの設定を変更することで自由に見た目を整えることができます。

Pythonで単純移動平均線【SMA：Simple Moving Average】を算出3

【フリーランス向けの完全無料Pythonプログラミング講座】

dot blogではこの記事以外にも完全無料でフリーランス向けのPythonプログラミング講座を公開中です。フリーランスとして活躍し稼ぐための強力な武器となりますよ。

Python入門講座【無料のプログラミング学習講座】

最近特に注目度が高くなってきているプログラミング言語Python。転職、フリーランス、独立・起業を検討中、日々の業務が忙しい社会人等は今こそ身に付けておきたいスキルの1つ。初心者向けにやさしいプログラミング学習内容のPython入門講座を無料で公開。

この記事を読む ≫